| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 맛집
- devops
- Spring
- elasticsearch
- jsp
- Gradle
- IntelliJ
- AWS
- jenkins
- MySQL
- db
- javascript
- Oracle
- java
- laravel
- JVM
- Spring Batch
- ReactJS
- 요리
- springboot
- ubuntu
- php
- Git
- it
- linux
- tool
- redis
- Design Patterns
- Web Server
- Spring Boot
- Today
- Total
아무거나
multi-variable linear regression 본문
multi-variable linear regression
Linear Regression(선형 회귀)

- Hypothesis
- 어떤 문제를 다루기 위해 가설, Hypothesis를 세움
- Cost function
- 해당 hypothesis를 검증하는 단계로써 cost function을 통해 cost를 계산
- Gradient descent algorithm
- cost를 최소화 하기 위해 Gradient descent algorithm 을 사용
이를 통하여 우리는 아래 이미지와 같은 하나의 input, 즉 하나의 변수에 대한 문제를 다루었다.
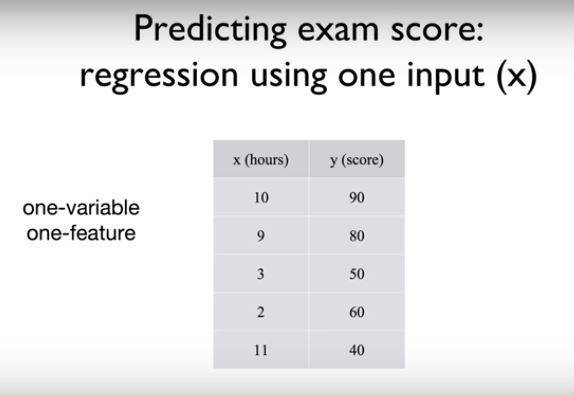
하나가 아니고 여러개의 input일 경우에는 multi-variable에 대한 문제가 존재

여기서 1개가 있을 경우에는 아래 이미지와 같이 계산하였지만
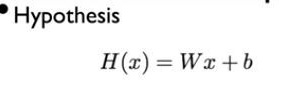
만약 3개가 있다고 가정하면 아래 이미지처럼 계산하면된다. 즉, 학습해야될 값이 증가한다.

Matrix(행렬)
위와 같은 식처럼 variable을 나열하는데에도 한계가 생김

이럴땐 행렬을 이용한다. (아래 이미지는 행렬 곱에 대한 개념)

Matrix을 이용한 필요한 Hypothesis를 표현하면 아래와 같다.

위의 식과 같이, 단순히 우리가 그전에 배웠던 hypothesis를 행렬로써 나타 그럼 이제 실제 데이터와 함께 생각해보면 우선 아래 이미지를 보면 3개의 x 변수가 있고 이에 따른 하나의 y변수가 있다. 좌측에 테이블을 보면 총 5쌍의 데이터를 볼 수 있는데, 이때 하나하나를 인스턴스라고 합다. (ex: 첫번째 인스턴스는 73, 80, 75, 152)

위의 다수의 인스턴스들을 행렬에서 매우 심플하게 정리하려면 각각의 인스턴스를 오른쪽의 식에 대입하는 것이 아니라, 아래의 사진과 같이 식을 변형한다.

위의 사진에서는 모든 인스턴스를 추가하며, w는 그대로 고정하였고 단순히 식으로써 나열하는 것보다 매우 깔끔하고 심플한 것을 볼 수 있다. 즉, 아래 이미지처럼 행렬을 이용한 hypothesis를 진행하게 된다.
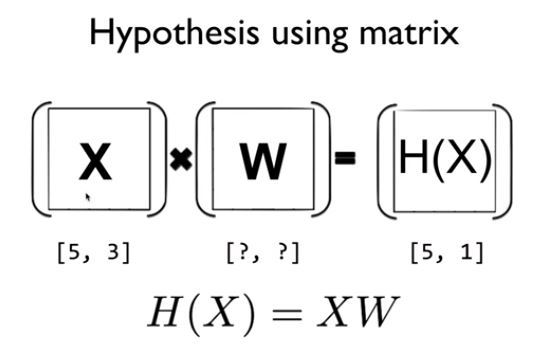
즉, 아래 이미지처럼 우리가 Python이나 Tensorflow로 위의 Linear Regression을 구현하려면 지금까지 배웠던 H(x) = Wx + b 로 계산하는 것이 아니고, H(X) = XW로 구현해야 한다.

'AI or APP > Tensorflow' 카테고리의 다른 글
| cost 최소화 알고리즘 설명 (0) | 2018.07.15 |
|---|---|
| Linear Regression (0) | 2018.07.04 |
| TensorFlow 설치 및 사용 (6) | 2018.06.22 |
| 머신러닝이란 (0) | 2018.06.18 |




